Смежные углы - это углы, которые имеют общую вершину и одну общую сторону, а две другие стороны лежат на одной прямой. Эти углы обладают важным свойством, которое позволяет легко вычислять их сумму.
Содержание
Основное свойство смежных углов
| Свойство | Описание |
| Сумма смежных углов | Всегда равна 180° (развернутому углу) |
Как определить смежные углы
Признаки смежных углов
- Общая вершина
- Одна общая сторона
- Две необщие стороны образуют прямую линию
Примеры на рисунке
| Ситуация | Являются ли углы смежными |
| ∠AOB и ∠BOC с общей стороной OB | Да, если стороны OA и OC лежат на одной прямой |
| ∠ABC и ∠DEF | Нет, разные вершины |
Формула суммы смежных углов
Если ∠1 и ∠2 - смежные углы, то: ∠1 + ∠2 = 180°
Вывод формулы
- Смежные углы вместе образуют развернутый угол
- Развернутый угол всегда равен 180°
- Следовательно, сумма смежных углов равна 180°
Практическое применение
Нахождение неизвестного угла
- Если известен один из смежных углов, второй вычисляется по формуле: 180° - известный угол
- Пример: если ∠1 = 45°, то ∠2 = 180° - 45° = 135°
Примеры решения задач
| Условие | Решение |
| Один смежный угол равен 70° | Второй угол = 180° - 70° = 110° |
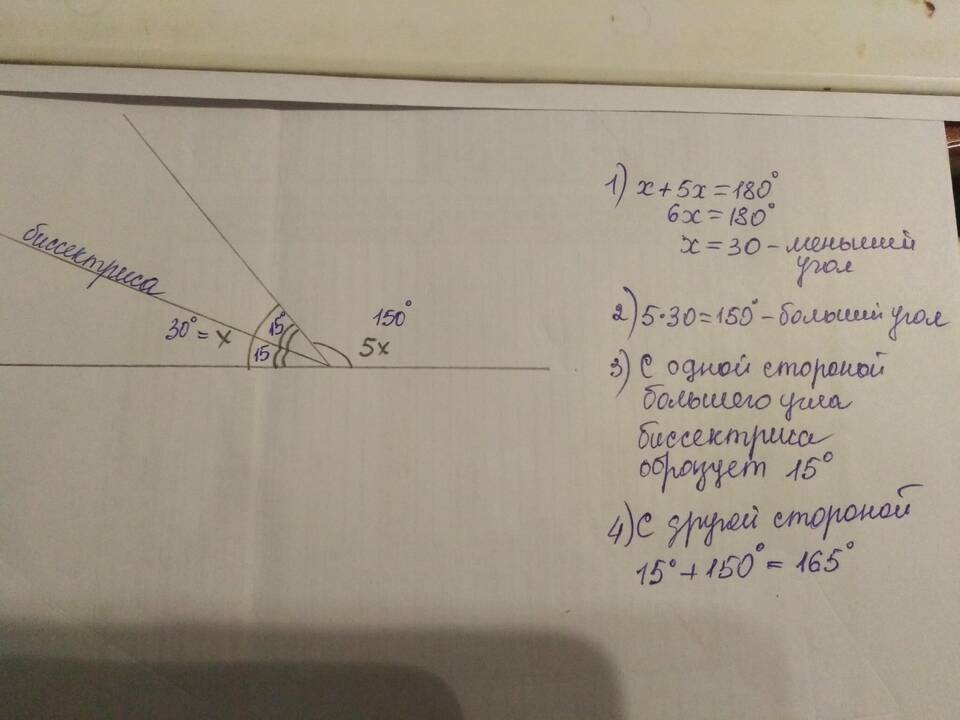
| Один угол в 3 раза больше другого | x + 3x = 180° ⇒ x = 45°, 3x = 135° |
Геометрические доказательства
Доказательство свойства смежных углов
- Пусть ∠AOB и ∠BOC - смежные углы
- Стороны OA и OC образуют прямую
- ∠AOC - развернутый угол = 180°
- ∠AOB + ∠BOC = ∠AOC = 180°
Использование в теоремах
- Доказательство равенства вертикальных углов
- Решение задач на параллельные прямые
- Построение перпендикулярных линий
Знание свойства смежных углов и умение находить их сумму - важный навык в геометрии, который применяется при решении различных задач и доказательстве теорем. Это фундаментальное понятие, на котором строятся многие геометрические законы.