Сумма первых n натуральных чисел - классическая задача математики, имеющая фундаментальное значение в алгебре и теории чисел. Решение этой задачи известно с древних времен и приписывается математику Карлу Фридриху Гауссу.
Содержание
Сумма первых n натуральных чисел - классическая задача математики, имеющая фундаментальное значение в алгебре и теории чисел. Решение этой задачи известно с древних времен и приписывается математику Карлу Фридриху Гауссу.
Формула суммы первых n чисел
| Формула | S = n(n + 1)/2 |
| Где |
|
Примеры вычислений
- Сумма первых 5 чисел: 1+2+3+4+5 = 15 = 5×6/2
- Сумма первых 10 чисел: 1+2+...+10 = 55 = 10×11/2
- Сумма первых 100 чисел: 1+2+...+100 = 5050 = 100×101/2
Доказательство формулы
Рассмотрим два способа доказательства:
| Метод Гаусса | Запишем сумму дважды: S = 1 + 2 + 3 + ... + n S = n + (n-1) + (n-2) + ... + 1 Сложим почленно: 2S = (n+1) + (n+1) + ... + (n+1) = n(n+1) |
| Математическая индукция | База: для n=1 формула верна Предположение: верно для n=k Шаг: докажем для n=k+1 |
Применение формулы
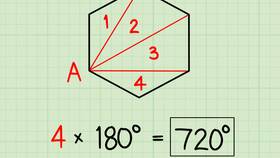
- Вычисление треугольных чисел
- Анализ алгоритмов в информатике
- Решение задач комбинаторики
- Финансовые расчеты (аннуитеты)
Обобщения формулы
- Сумма квадратов: n(n+1)(2n+1)/6
- Сумма кубов: [n(n+1)/2]²
- Сумма арифметической прогрессии: (a₁ + aₙ)n/2
Формула суммы первых n натуральных чисел является базовой в математике и находит многочисленные применения в различных областях науки и техники.
